Sin embargo, no faltan propuestas, siendo sin duda alguna la más popular la teoría de cuerdas. Esta teoría se basa en la idea de que las materia está conformada por filamentos de energía que están en vibración. Dicha teoría requiere para su consistencia interna la presencia de un número de dimensiones mayor de cuatro (10 u 11 según la versión de teoría de cuerdas que empleemos) y la presencia de supersimetría. La supersimetría relaciona partículas con espín entero con compañeras de espín semientero y viceversa. A día de hoy no hay pruebas experimentales ni de las dimensiones extra ni de los compañeros supersimétricos de las partículas que conocemos. Pero está claro que el esquema presentado por teoría de cuerdas, a pesar de los detalles comentados, es muy sugerente porque permite unificar en una única teoría todas las partículas conocidas y todas las interacciones, incluyendo la gravedad y todo esto a nivel cuántico. No queremos hablar en esta entrada de esta teoría, que ha sido tratada extensamente en muchos sitios presentando sus virtudes y sus problemas. Más bien lo que queremos es presentar, sencillamente, las bases de una teoría de gravedad cuántica que se ha venido desarrollando desde mediados de los años 80 del siglo anterior.
La teoría anteriormente mencionada se la conoce en castellano como Gravedad Cuántica de Lazos (algunos prefieren Bucles). En esta entrada nos referiremos a ella como Loop Quantum Gravity que es su nombre en inglés y generalmente emplearemos LQG para referirnos a ella.
¿En qué se basa LQG?
La motivación de la LQG es simple, combinar las teorías actuales de gravedad con la mecánica cuántica.
La gravedad viene descrita por la Relatividad General (RG en lo que sigue) y nos dice que la gravedad no es más que la respuesta del espaciotiempo a la presencia de cualquier otro campo (electromagnético, fuerte, etc). La gravedad es la manifestación del cambio de la geometría del espaciotiempo como respuesta a la presencia de energía en el mismo (y a como esté distribuida).
Según la RG la gravedad no es una fuerza ni una interacción. Es algo mucho más especial, es la manifestación de la propia geometría del espaciotiempo y esta geometría es dinámica. Esto implica que responde a la presencia de materia y energía. Y claro, si la geometría cambia, la forma de propagarse la materia y la energía también cambia. La relación entre geometría y energía presente en el espaciotiempo es lo que condensan las ecuaciones de Einstein de la RG.
Cuando hablamos de geometría esencialmente nos referimos a eso, a como medir longitudes, áreas, volúmenes etc. Y la geometría está condensada en un objeto matemático denominado métrica, que para lo que nos interesa es lo que nos permite medir los conceptos anteriormente mencionados. Por tanto RG nos dice que la métrica es algo que cambia cuando hay energía y/o materia en una región del espaciotiempo. El típico ejemplo de la sabana que se curva porque ponemos un cuerpo con masa es bastante bueno y aunque no es totalmente fiel a la teoría sí que nos da una idea acerca de lo que ocurre.
La conclusión aquí es simple:
RG trata del propio espaciotiempo, de su comportamiento como un objeto físico dinámico.
Esto es tan así que lo que se está buscando con las ondas gravitacionales son ondulaciones del propio espaciotiempo.
Si ahora queremos cuantizar, es decir encontrar la versión cuántica, la gravedad escrita como RG lo que tenemos que hacer es encontrar la teoría cuántica para la métrica. Sin embargo, esto no conduce a una teoría apropiada, surgen muchos problemas para dar sentido a esta teoría, aparecen infinitos y peor que eso, muchos cálculos no tienen ni tan siquiera un sentido claro. Así que hay que buscar otra forma de intentar llegar a la teoría cuántica. Y la clave está en los potenciales.
En las teorías de las interacciones no gravitatorias (electromagnética, débil, fuerte) los potenciales son esenciales (de forma más técnica empleamos potenciales gauge que se presentan como conexiones en el sentido matemático).
En este punto necesitamos otro concepto bien conocido, las líneas de campo. Este concepto fue introducido por Michael Faraday. Uno puede visualizar el campo como constituido por infinitas líneas que marcan por donde va el campo. Evidentemente uno no puede considerar infinitas líneas, así que en general elegimos un número finito (y fijado) de líneas para representar el campo.
Pero se puede tomar otra perspectiva. Imaginemos que el campo sólo está definido en esas líneas, un número finito de ellas. Y el potencial sólo está definido en los puntos de ese campo. Evidentemente para conocer el campo en su totalidad hay que conocer la infinitas líneas de campo y cuando vale el potencial en todos los puntos de dichas líneas. Pero uno siempre puede descomponer este conjunto de infinitas líneas en sumas de situaciones descritas por distintos números de líneas.
LQG llega a la misma conclusión, cuando fuerzan a la RG a ser cuántica, la teoría te dice que sólo puedes obtener información en líneas de campo (técnicamente en Wilson Loops). En este caso las líneas son cerradas, son círculos y de ahí viene el nombre de bucle o lazo (loop es más apropiado y el matiz en inglés en distinto a las palabras castellanas por las que se traducen). Esto implica que LQG predice una “discretización” efectiva del espaciotiempo, ya no se puede sondear en cualquier sitio, sólo tiene sentido hablar de gravedad (y por tanto del espaciotiempo y por donde se propagan partículas y energías) en esos loops.
¿Dónde están esos loops?
Esos loops no están en ningún sitio, esos loops definen el propio espaciotiempo por el cual la materia se propaga. Así que no tiene sentido de hablar del “espacio” donde están definidos los loops. Sólo tiene sentido hablar de dichos loops. Es decir, que a nivel cuántico un estado cuántico del espacio está dado por una configuración de dichos loops. No tiene sentido hablar de lo que hay fuera de los mismos.
Pero pronto se descubrió que este procedimiento era ciertamente complicado a la hora de hacer cálculos. Y se encontró una simplificación, las redes de espín (a las que nos referiremos como espín networks).
Espín Networks
Sorprendentemente la respuesta se encontró en los espín networks, que fueron introducidos por Roger Penrose para dar una definición cuántica del espacio, sin embargo no fueron muy populares porque no se deducían de primeros principios y en esencia era una construcción introducida a mano. Casualmente LQG recuperó este concepto partiendo de los principios de la relatividad general combinados con la cuántica.
Los espín Networks son simplemente grafos, conjunto de líneas unidas en nodos, donde cada línea del grafo tiene una etiqueta que puede tomar valores 1/2, 1, 3/2, 2, 5/2,…
Estas líneas tienen una orientación, es decir, podemos decir si la línea “entra” a un nodo o “sale” del nodo dado. Además, los nodos también tienen información, en ellos hay un objeto matemático que transforma los valores de las etiquetas entrantes en los valores de las etiquetas salientes, correspondientes a las líneas entrantes y salientes de un nodo dado. Esta es una característica esencial de la teoría.
El punto esencial es que dado un conjunto de loops siempre se puede encontrar un espín network equivalente.
Los estados cuánticos del espaciotiempo, o de la geometría siguiendo las enseñanzas de RG, vienen dados por un espín network (conjunto de líneas unidas en los nodos y las etiquetas de cada línea). Es por eso que a veces se dice que los espín networks representan un estado cuántico de la geometría y por eso también se suele llamar a LQG, Geometría Cuántica.
Geometría en LQG
Es evidente que si queremos hablar de geometría hemos de dar la receta para medir longitudes, ángulos, áreas o volúmenes. LQG da dichas recetas y se encuentra un resultado sorprendente. Aquí presentamos únicamente el área porque es el caso más simple y el mejor conocido.
Si queremos calcular el área de una superficie dada, S, lo que tenemos que hacer es mirar cuantas líneas de un espín network la “pinchan”. Entonces miramos las etiquetas asociadas y una determinada función de dichas etiquetas nos da el valor del área.
Para concretar, supongamos que la superficie S únicamente está “pinchada” por un lado del espín network. Dicho lado tiene una etiqueta de valor j. El área de la superficie S viene dada por esta expresión:
Lo que implica esto es que las áreas no pueden tomar cualquier valor, existe un mínimo de área que viene dada por el valor j=1/2. Evidentemente si tenemos muchos lados “pinchando” el área vendrá dada por la suma de las correspondientes raíces cuadradas de las etiquetas j de cada lado que “pincha” la superficie de interés.
Para volúmenes, longitudes y ángulos también es conocido que no pueden tomar más que ciertos valores. Así que en cierto sentido la geometría del espaciotiempo está discretizada.
Un último comentario sobre esta fórmula, y por ende de la teoría entera. En LQG tenemos un parámetro, un número real, denominado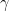
que es el parámetro de Barbero-Immirzi (Fernando Barbero puede ser considerado uno de los padres de esta teoría, y actualmente es un investigador del CSIC). No hay restricción alguna al valor de este parámetro, únicamente ha de ser distinto de cero. Así que hay que fijar su valor de alguna forma. Hasta la fecha no hay un consenso sobre el valor o el papel que juega el parámetro de Barbero-Immirzi en la teoría.Preguntas sobre LQG:
¿Cuál es el mayor problema de la LQG?
El principal problema de la LQG es que no se sabe si cuando revertimos el proceso de convertirla en una teoría cuántica volvemos a obtener RG.
Cuando uno tiene una teoría cuántica, un criterio de consistencia es calcular el límite clásico, es decir, lo que nos queda cuando revertimos el proceso de cuantización ha de ser la teoría clásica correspondiente.
Veamos este esquema:
Partimos de una teoría clásica A, efectuamos el proceso de cuantización, obtenemos la teoría cuántica A, que llamaremos qA. Ahora revertimos el proceso, lo que se llama límite clásico de la teoría qA, y miramos a ver si acabamos otra vez en A.
Teoría clásica A —(cuantización)—> Teoría qA —(límite clásico)—> Teoría clásica A
Para el electromagnetismo esto funciona perfectamente:
Electromagnetismo de Maxwell —> Electrodinámica Cuántica —-> Electromagnetismo de Maxwell.
Evidentemente en el proceso de límite clásico la teoría cuántica te dice que hay diferencias con la teoría clásica pura, lo que se llaman correcciones cuánticas, pero que tales correcciones son muy pequeñas y no perceptibles a las escalas de energías y velocidades usuales del mundo clásico (aquel que no es relativista ni cuántico, nuestro día a día).
Para LQG lo que tenemos es:
Relatividad General —> Loop Quantum Gravity —> ¿¿¿???
Hasta que los físicos trabajando en este tema no prueben que de hecho se recupera RG (con correcciones cuánticas) la LQG no es útil.
¿Es LQG una teoría unificadora?
La respuesta inicial es no. LQG puede aceptar cualquier tipo de campo no gravitatorio viviendo sobre los espín networks. Así que no hay restricciones ni unificaciones. Sin embargo, hay una unificación sutil en LQG, en esta teoría la gravedad se formula de manera idéntica al resto de interacciones del modelo estándar de la física de partículas.
Además, no sabemos si la teoría puede dar mayores pistas a la unificación porque aún no conocemos la teoría en su totalidad. Habrá que esperar a mayores avances.
¿Puede ser formulada LQG en un espaciotiempo con un número de dimensiones mayores de cuatro?
Pues hasta hace poco la respuesta era no, pero desde Mayo de este año hay una versión de la teoría que permite extender las técnicas de LQG a un número arbitrario de dimensiones. Además permite introducir supersimetría en este contexto en dimensiones extra. Esto puede ser útil para ver si LQG y Teoría de Cuerdas tienen algún punto en común.
¿Cuáles son los motivos para seguir investigando en LQG?
El principal es que el tema es interesante y que es ciertamente complicado. Además de que hay resultados parciales que indican que se está en el buen camino. Los resultados más prometedores son:
– En LQG se puede calcular la entropía de los agujeros negros. Si bien es cierto que inicialmente para encontrar la ley de Bekenstein-Hawking que dice que la entropía de un agujero negro es A/4, para encontrar el coeficiente 1/4, hay que fijar un parámetro libre de la teoría para acomodar este valor. Esto parece un poco ad hoc, pero actualmente los últimos resultados indican que no hay que fijar dicho parámetro para encontrar la proporcionalidad correcta entre entropía y área en un agujero negro. Hay que comentar que LQG permite calcular la entropía de agujeros negros pausibles en astrofísica.
– Cuando se importan las técnicas de LQG a la cosmología se encuentra que la singularidad inicial del universo, el punto inicial del big bang, no es un punto especial. El universo fluye por dicho estado inicial de forma suave. Esto es lo que ha dado lugar a la teoría del big bounce o el gran rebote. Lo que viene a decir es que nuestro universo tuvo un universo previo que colapsó y rebotó en lo que nosotros llamamos big bang.
– Las preguntas que surgen son muchas, ¿qué era ese universo? ¿era igual que el nuestro pero colapsando? ¿de donde surgió?. Todas estas preguntas se están investigando y no hay una respuesta clara. Pero además se están buscando señales susceptibles de ser observadas en la radiación cósmica de fondo, y por tanto someter esta teoría al escrutinio de la experiencia, que proceden de este modelo de evolución del universo. Posiblemente esta teoría cosmológica basada en LQG, que se conoce como LQC, afecte a la teoría inflacionaria, y por tanto podrá ser discriminada por observaciones cosmológicas que cada día son más precisas.
Fuente NAUKAS